Die Polare

Die Polare ist die Abbildung eines Punkte $P_{0}$ (zunächst einmal ausserhalb eines gegebenen Kreises) auf eine Gerade g¹ (in der Dimension 2, Ebene in Dim 3 …) , die diesen Kreis so schneidet, dass die Schnittpunkte die Berührpunkte der beiden von $P_{0}$ an den Kreis gezogene Tangenten sind !

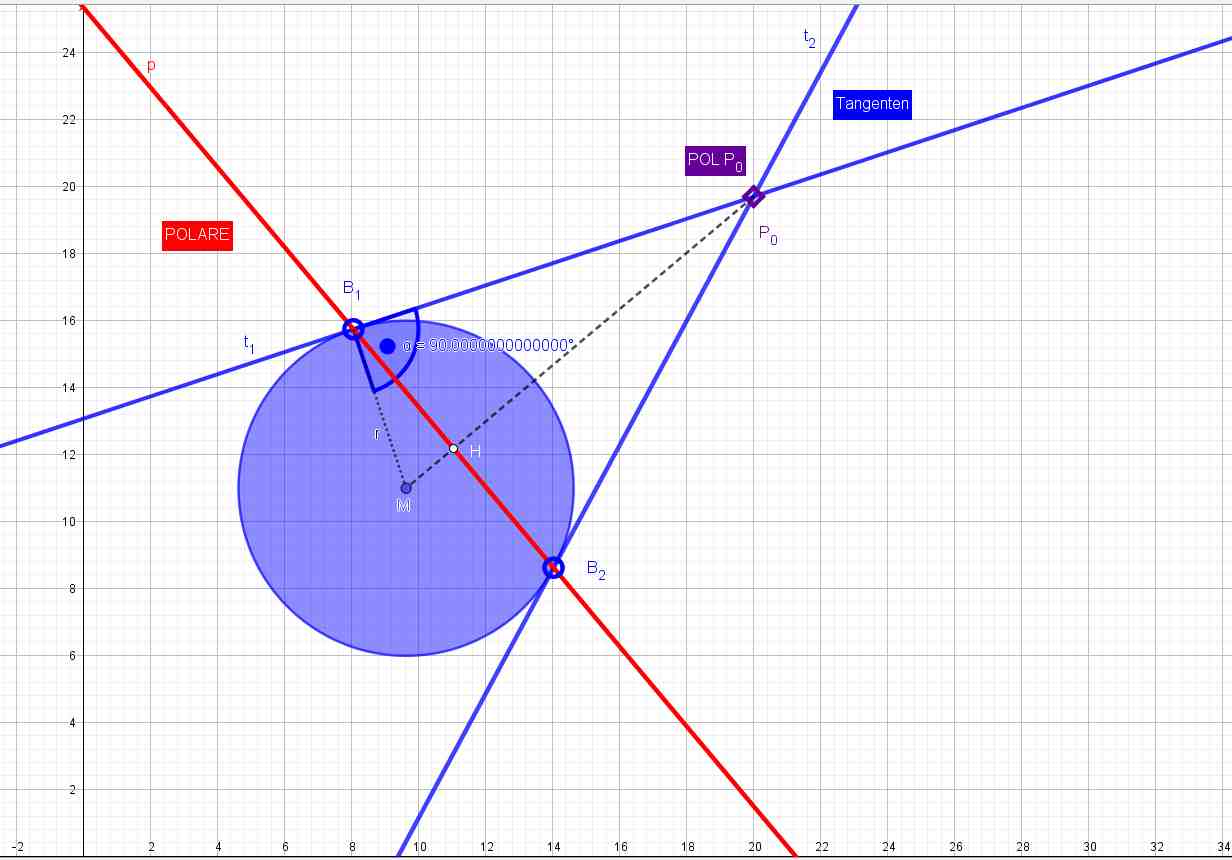
Die Gleichung der POLAREN zum Pol $P_{0}$:

O.B.d.A. legen wie den Kreismittelpunkt in den Ursprung (Verschiebung des Koordinatensystems um den Vektor -xM)! Die Polarengleichung beschreiben wir in der Normalenform $$\boldsymbol{n} \cdot (\boldsymbol{x} – \boldsymbol{x_g}) = 0$$

wobei $\boldsymbol{n}$ Normalenvektor, der Ortsvektor zum Pol $\boldsymbol{P_{0}}$ und $\boldsymbol{x_{g}}$ ein beliebiger Punkt der zu beschreibenden Polaren-Geraden (z.B. die Mitte $H$ der Berührpunktverbindung) ist! $$\boldsymbol{n_{0}} \cdot \boldsymbol{x} = d$$ wobei $\boldsymbol{n_{0}}$ der Einheitsnormalenvektor ist, den man durch die Teilung von $\boldsymbol{n}$ durch die Länge von $n = | \boldsymbol{n} | = | \boldsymbol{P_0} |$ erhält, und $d = \boldsymbol{n}_{0}\boldsymbol{x}_g$ der Abstand der Geraden zum Ursprung ist. Nun ist der senkrecht auf der Polaren stehenden Normalenvektor $\boldsymbol{n} = \boldsymbol{x_{P_0}}$ der von der Kreismitte zum Pol $\left( x_{P_0}; \: y_{P_0} \right)$ verlaufende Ortsvektor. Da seine Länge $|\boldsymbol{x_{P_0}}| =\sqrt{( x_{P_0}^2 + y_{P_0}^2)}$ gerade die Länge des Ortsvektors $\boldsymbol{x_{P_0}}$ ist, der von der Kreismitte bis zum Pol verläuft, müssen wir dir Normalenform durch diese Länge teilen um den Abstand d der Polaren um Ursprung zu erhalten. Nun ist aber das Produkt von $d$ mit der Länge $|\boldsymbol{x_{P_0}}|$ nach dem Kathetensatz des Euklid gerade das Quadrat der Kreisradius $r^2$ $$d \cdot \sqrt{( x_{P_0}^2 + y_{P_0}^2)} = r^2$$ und daher hat man statt der HNF: $\boldsymbol{n_0}\cdot\boldsymbol{x} = d$ $$\boldsymbol{x}_{P_0}\cdot\boldsymbol{x} = r^{2}$$ $$x_{P_0}\cdot x + y_{P_0}\cdot y = r^2$$ Wenn der Pol $\boldsymbol{P_0}$ ein Punkt der Kreislinie ist, liegt der Pol auf der Polaren und ist Berührpunkt $B(x_b; y_b)$.

Berechnen wir nun zu zwei gegebenen Berührpunkten den Pol bzw zu drei Berührpukten die Ecken des Dreiecks. Hier nütze ich nun die Gelegenheit, die mit Abstand beste Methode zur Auflösung linearer Gleichungssysteme vorzustellen: Die Determinantenmethode! Es ist nämlich ein handfester Skandal, dass Determinanten in der Schule nicht mehr unterrichtet werden. Es gibt nichts besseres, wenn man am sichersten, schnellsten und effektivsten lineare Gleichungssysteme auflösen will !!!

Seien nun $B_1(x_1; y_1)$ und nun $B_2(x_2; y_2)$ zwei Berührpunkte am Einheitskreis (sonst die $1$ durch $r^2$ ersetzen!), dann sind die $$1.\qquad x_1x+y_1y=1 \enspace bzw. \enspace r^2$$ $$2.\qquad x_2x+y_2y=1 \enspace bzw. \enspace r^2$$
Die Lösung für $x$ und $y$ sind die Quotienten zweier Determinanten: Zählerdeterminante $Z_x$ bzw. $Z_y$ durch die Nennerdeteminante $N$ wobei die Nennerdeterminante $N$ einfach diejenige der Koeffizienten der Variablen ist $$N=\left| \begin{array}{rr} x_1 & y_1 \\ x_2 & y_2 \\ \end{array}\right|=x_1y_2-y_1x_2 $$ Wenn diese Nennerdeteminante nicht verschwindet, gibt es immer genau eine eindeutige Lösung! Für die Zählerdetemimnate ersetzt man die Variablenspalte durch die Spalte der absoluten Glieder, die auf der anderen Seite des Gleichheitszeichnes stehen, was hier eine Einserspalte ist: $$Z_x=\left| \begin{array}{rr} 1 & y_1 \\ 1 & y_2 \\ \end{array}\right|=y_2-y_1$$
$$Z_y=\left| \begin{array}{rr} x_1 & 1 \\ x_2 & 1 \\ \end{array}\right|=x_1-x_2$$
$$x=\frac{(y_2-y_1)}{N}$$
$$y=\frac{(x_1-x_2)}{N}$$
Folgerung:
Sind die Koordinaten der Inkreis-Berührpunkte rational, sind auch die Koordinaten der Ecken rational.

Beispiel:
Die Berührpunkte sind $(0.8;\;0.6)$ und $(0;\;-1)$ $$N=\left| \begin{array}{rr} 0.8 & 0.6 \\ 0 & -1 \\ \end{array}\right|=-0.8-0=-0.8$$ $$x=(y_2-y_1)/N=((-1)-0.6)=-1.6/(-0.8)=2$$ $$y=(x_1-x_2)/(-0.8)=(0.8-0)/(-0.8)=-1$$ Den Pol (die Ecken) bekommt man durch die Kreisspiegelung der Verbindungsmitte der beiden Berührpunkte!
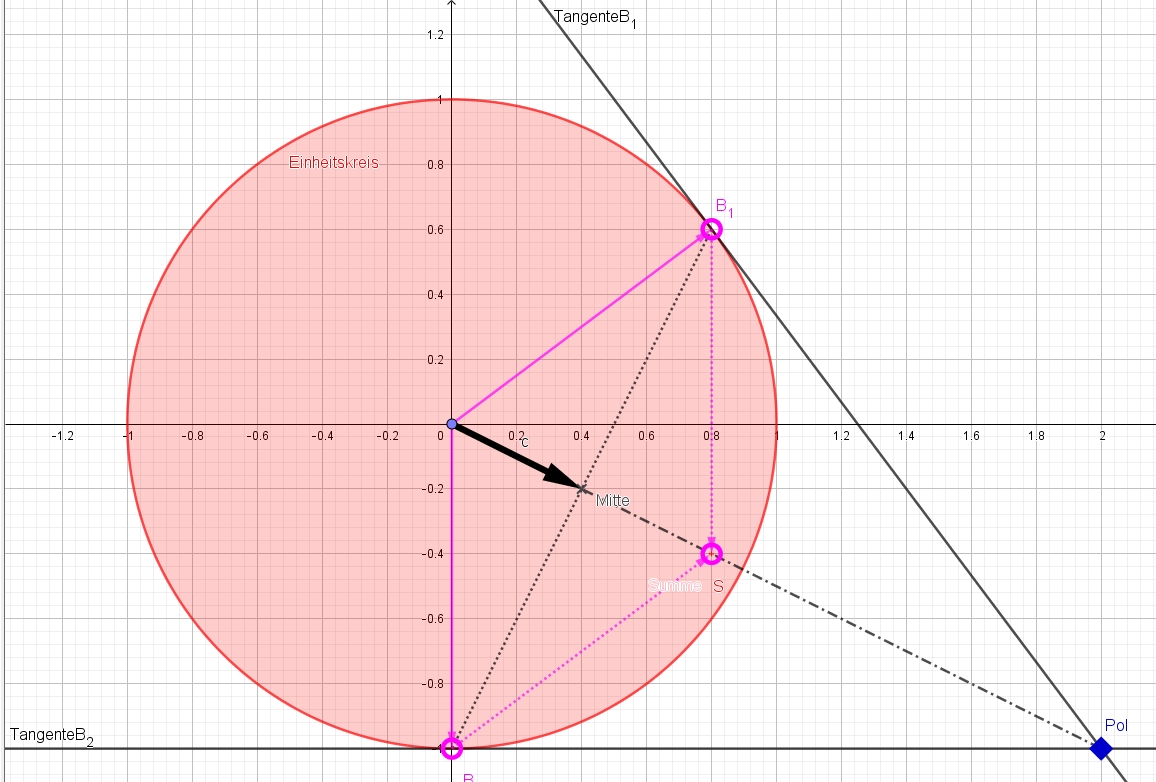
Am Einheitskreis ist das Produkt der Längen von Gegenstandspunkt und Bildpunkt gerade $1$ (allgemein $r^2$), so dass die Entfernung zum Pol gerade der Kehrwert der halben Vektorsumme der Berührpunte (Verbindugsmitte) ist. Der Summen-Vektor $(0.8;\;-0.4)$ hat die Länge $\sqrt{.8^2+.4^2}=\sqrt{.8}=\sqrt{4/5}=2\sqrt{5}$. Der halbe Summenvektor hat also die Länge $\sqrt{5}$. Der Kehrwert davon ist $\frac{1}{\sqrt{5}}=\sqrt{5}$, und der Pol $(2;\;-1)$ ist genau $\sqrt{1^2+0.2^2}=\sqrt{5}$ entfernt!

Beweise:

1. Die Länge des Tangentenabschnitts $t=B_iP_0$ ist gleich dem Produkt der Länge vom Ursprung zu $P_0$ und der halben Entfernung der Berührpunkte $B_1B_2$ (= der doppelten Fläche $2A$ des rechtwinkligen Drachens $OP_0B_1B_2$!)2 In der Abb. ist $t=2$ und $OP_0=\sqrt{5}$ und die andere Diagonale hat die Entfernung der Berührpunkte $B_1B_2$ $|(0.8;0.6)-(0;-1)|=\sqrt{32}=4\sqrt{5}$
2. In komplexer Schreibweise ist der Pol $P_0=(B_1 \cdot B_2) / [\frac{1}{2}(B_1 + B_2)]$
   Anleitung: Zeige, dass die Länge und der Winkel übereinstimmen 3
Komplex berechnet sich der Pol als verdopplete Wehrle-Zahl der beiden Berührpunkte; was dasselbe wie Produkt duch die halbe Summe ist: Das Produkt ist doch das Minus-i –fache von $(0.8; 0.6)$: $( 0.8i – 0.6 ) = 0.6 - 0.8i$ (Drehung um $-90$ Grad)
Produkt durch halbe Summe also $$(0.6 -0.8i) /( 0.4-0.2i) =$$ $$(0.6 -0.8i) ( 0.4+0.2i) \; / \; Längenquadrat=0.2$$ $$0.24 + 0.16 - 0.32i +0.12i \; / \;Längenquadrat=1/5$$ $$( 0.4 – 0.2i ) \cdot 5 = 2 - i$$

Hinweis zu den Fussnoten: Einfach auf die Fussnoten im Text klicken und es klappt sich ein Text auf, mit der Erkärung zur der Fussnote.